Emergence of Unitarity and Locality from Hidden Zeros at One-Loop
25th September, 2025
Laurentiu Rodina, Associate Professor at the Beijing Institute of Mathematical Sciences and Applications (BIMSA), together with PhD student Jeffrey Backus (Princeton University), has published a paper in Physical Review Letters titled “Emergence of Unitarity and Locality from Hidden Zeros at One-Loop.” The paper presents the first demonstration that two fundamental principles of quantum field theory—locality and unitarity—can emerge from deeper mathematical structures, even when quantum corrections from loops are included. This long-sought result resolves a problem regarded as both prohibitively difficult and conceptually elusive, representing a decisive step in showing that the core principles of quantum field theory (QFT) can in fact be derived rather than assumed.
At the heart of the paper are scattering amplitudes—the quantities that determine the probabilities of particle collisions. Traditionally, these amplitudes are built on two basic principles:
• Unitarity, the quantum rule that probabilities must always add up to one.
• Locality, the relativistic requirement that no influence can travel faster than light.
Together, these principles define QFT, the framework underpinning the Standard Model of particle physics. Yet Rodina’s earlier work revealed something unexpected: in various theories, including Yang–Mills or gravity, scattering amplitudes can be uniquely determined from only a minimal set of hidden constraints, with locality and unitarity emerging automatically. This was a radical departure from conventional wisdom. What were long thought to be the bedrock axioms of QFT — the very rules needed to define the theory — turn out instead to be consequences of deeper mathematical structures. The result is as unexpected as it is profound: it challenges the standard hierarchy of principles and points toward a more fundamental way of understanding QFT.
These previous results, however, had a major drawback: they applied only at the tree level—the simplest scattering processes without quantum corrections. Extending them to the loop level, the next order in perturbation theory, where virtual particles circulate and amplitudes grow vastly more complicated, was long viewed as nearly impossible. At this level, even the basic notion of uniqueness seemed ill defined, since different integrands can lead to the same final result after integration. Establishing uniqueness and emergence at loop level thus became a problem of both high difficulty and significant importance.
This new paper overcomes these obstacles. It shows that a property called hidden zeros—special kinematic configurations where amplitudes unexpectedly vanish—not only survives at loop level but is powerful enough to uniquely determine one-loop integrands in certain theories. This extends Rodina’s earlier tree-level results into the quantum regime, establishing that scattering amplitudes in QFT are determined entirely by a single underlying principle, with locality and unitarity following as unavoidable consequences, even beyond leading order in perturbation theory.
To achieve this, they employ the “surface kinematics” formalism, a framework that reformulates scattering amplitudes in terms of combinatorial structures associated with triangulations of punctured disks.
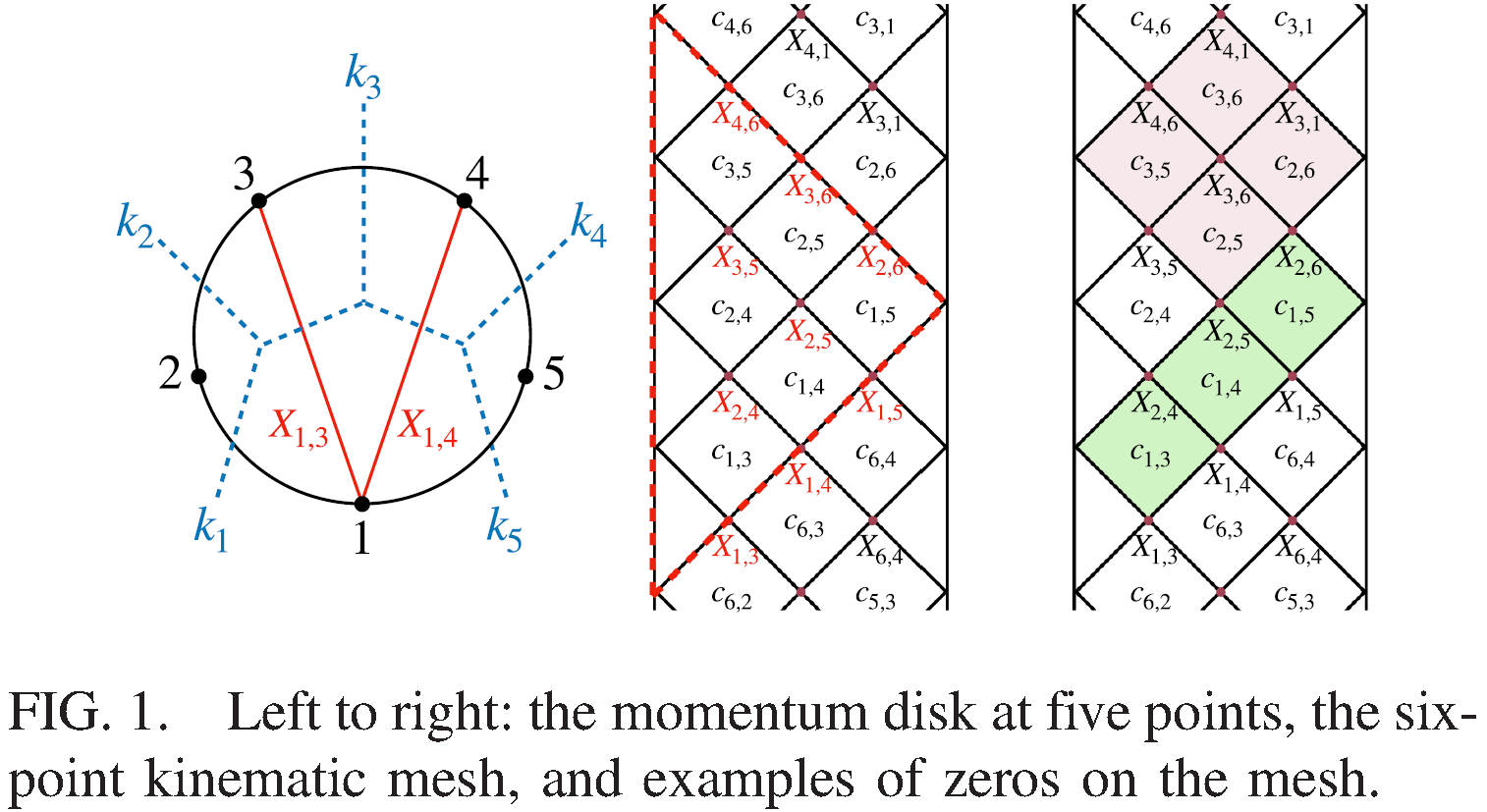
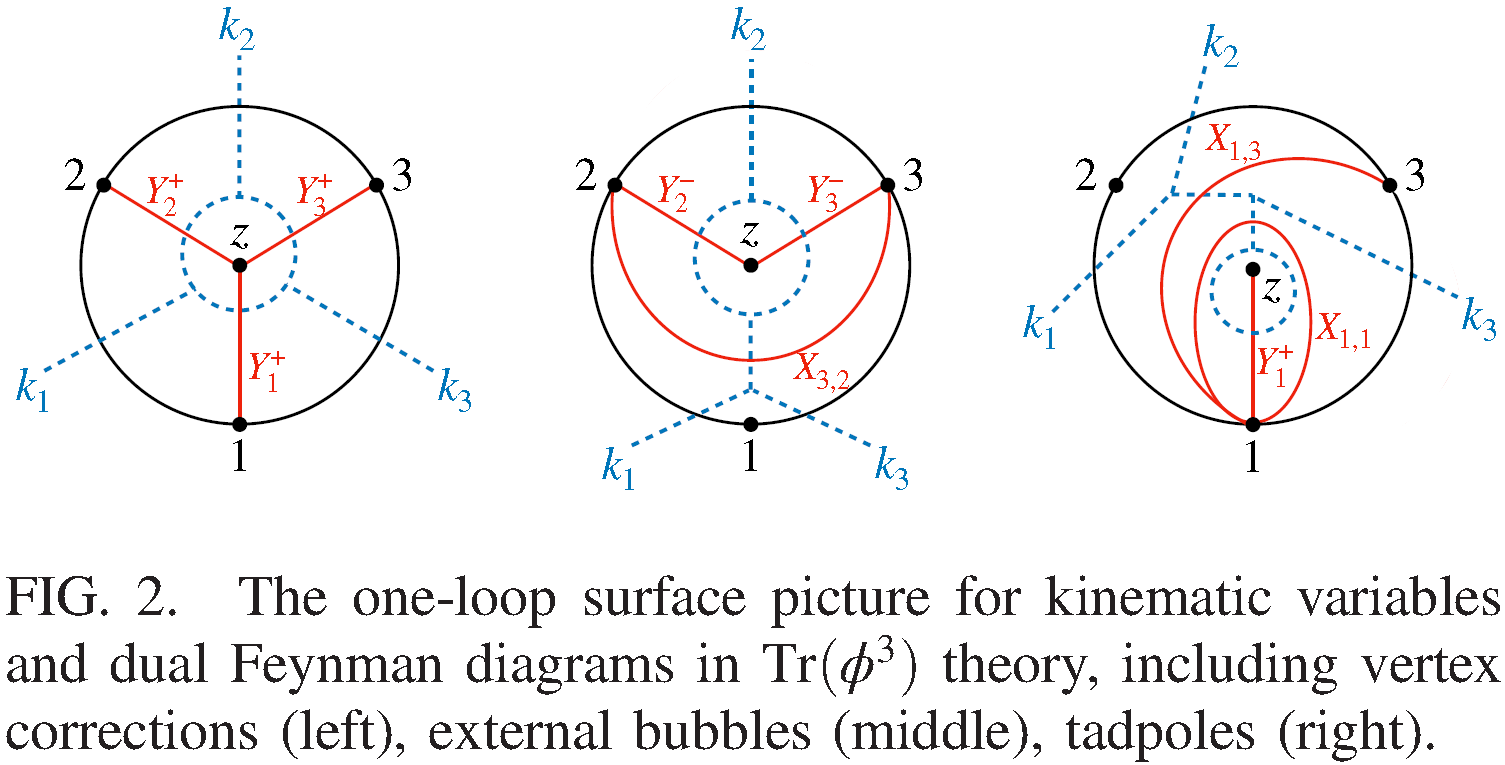
Looking further ahead, the implications connect naturally to expectations from quantum gravity, where both locality and unitarity are anticipated to take radically new forms. If we are to uncover how these principles emerge in a complete theory of gravity, it is essential to first master their emergence within the more familiar and established setting of QFT. This paper provides a decisive step in that direction.
Rodina’s work is supported by the NSFC General Program No. 12475070, and the BJNSF Project No. IS24014.





