New and efficient approach to classical simulations of variational quantum algorithms developed by Zhengwei Liu and his group

Recently, professor Zhengwei Liu, a principal investigarot (PI) for the Quantum Symmetries group at BIMSA, together with an assistant researcher Song Cheng and doctoral students Yuhe Shao and Fuchuan Wei at the Yau Mathematical Sciences Center (YMSC), has developed an efficient method for computing expectation values in noisy quantum circuits. This variational quantum algorithm, named "Observerable's back-propagation on Pauli paths (OBPPP)", was shown to have superior speed and accuracy in comparison to existing quantum hardware, and can be applied to a wide range of quantum circuits.

Quantum computation is currently in the "noisy intermediate-scale quantum (NISQ) era". As such, with its noise-tolerance and low requirements for quantum resources, variational quantum algorhithms have been developed to excel in real and meaningful applications of quantum computation. They have garnered much attention recently in the fields of combinatorial optimization, quantum chemistry, material computing and even machine learning. Despite this, variable quantum algorithms research still faces many questions, such as decoherence due to circuit noise, limitations on expressitivity, and the loss of trainability. In fact, finding a relatively classical variational quantum algorithm with truly quantum advantages is still a difficult open problem, that has been repeatedly discussed in the scientific community. Conversely, an equally important question is: "what kind of variational quantum algorithms are easy to be classically simulated?"

Towards this question, the Quantum Symmetries group at BIMSA has proven in theory that a large class of variational quantum algorithms in fact do not have quantum advantage in its architecture. Based on this finding, they have creatively developed a practical classical algorithm, the OBPPP, which has polynomial computational complexity. This algorithm was also compared with the aforementioned variational quantum algorithm, with favourable results.

(figure; caption: Left: schematic diagram of a noiseless quantum circuit. Right: schematic diagram of a noisy quantum sircuit.)

This work examines quantum circuits composed of Clifford gates and single-parameter Pauli rotation gates (depicted as white and pink in the above figure). This setup includes most of the current variational quantum circuit architechtures. This work can be applied to  various most commonly seen noise channels in experiments, for example the depolarizing noise and the dephasing noise, which are modeled by independent single-bit Pauli noise channels. The authors believe that this model can also be easily generalized to study a wider class of noises.

Based on the above model for the commly-seen variational quantum circuits, the researchers found that, when the circuit was expanded in the Pauli basis and the observables expressed as path integral summations, the speed of classical simulations for existing variational quantum algorithms are greatly improved. This method is advantageous for two important reasons: First, for general quantum circuits composed of Clifford gates and arbitrary-qubit single-parameter Pauli gates, the number of terms in this basis expansion are often less than traditional methods (such as the state vector method in the summation of tensor networks). Second, for noise channels modelled by single-parameter Pauli gates, the contribution of multiple noise terms are suppressed, and the suppression coefficient has a clear formula:

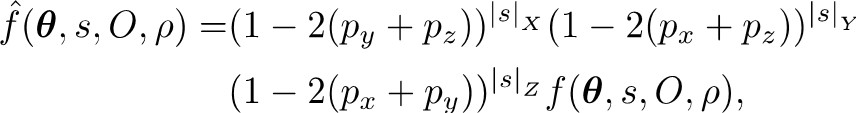
This ensures that, for each given finite error tolerance, the complexity of the algorithm depends is only polynomial in the number of qubits and the depth of the quantum circuit.

More precisely, the researchers have proved explicit formulas for the complexity of the classical simulations for these kinds of Pauli-type noisy quantum circuits. To be explicit, for a given error tolerance, the time complexity fit into the following two cases:

Case 1

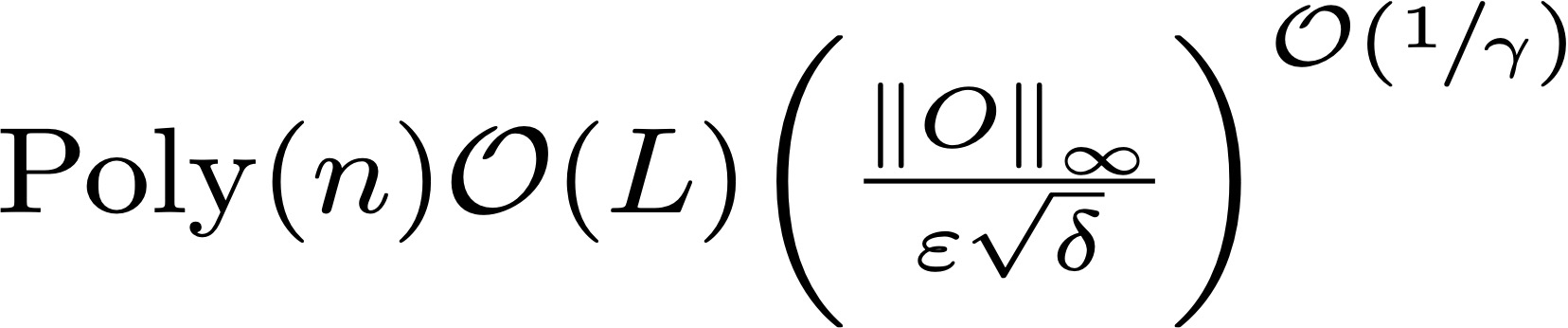
Case 2

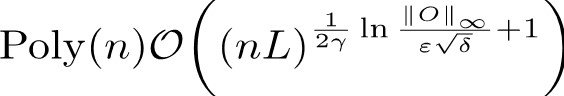
where n is the number of qubits, L is the depth of the circuit, epsilon is the error tolerance, and Gamma is the noise rate.

In fact, at a constant non-zero noise rate, the spacetime complexity of OBPPP depends only polynomially on the qubit number n and circuit depth L. Whereas in general quantum circuits, this is usually an exponential scaling.

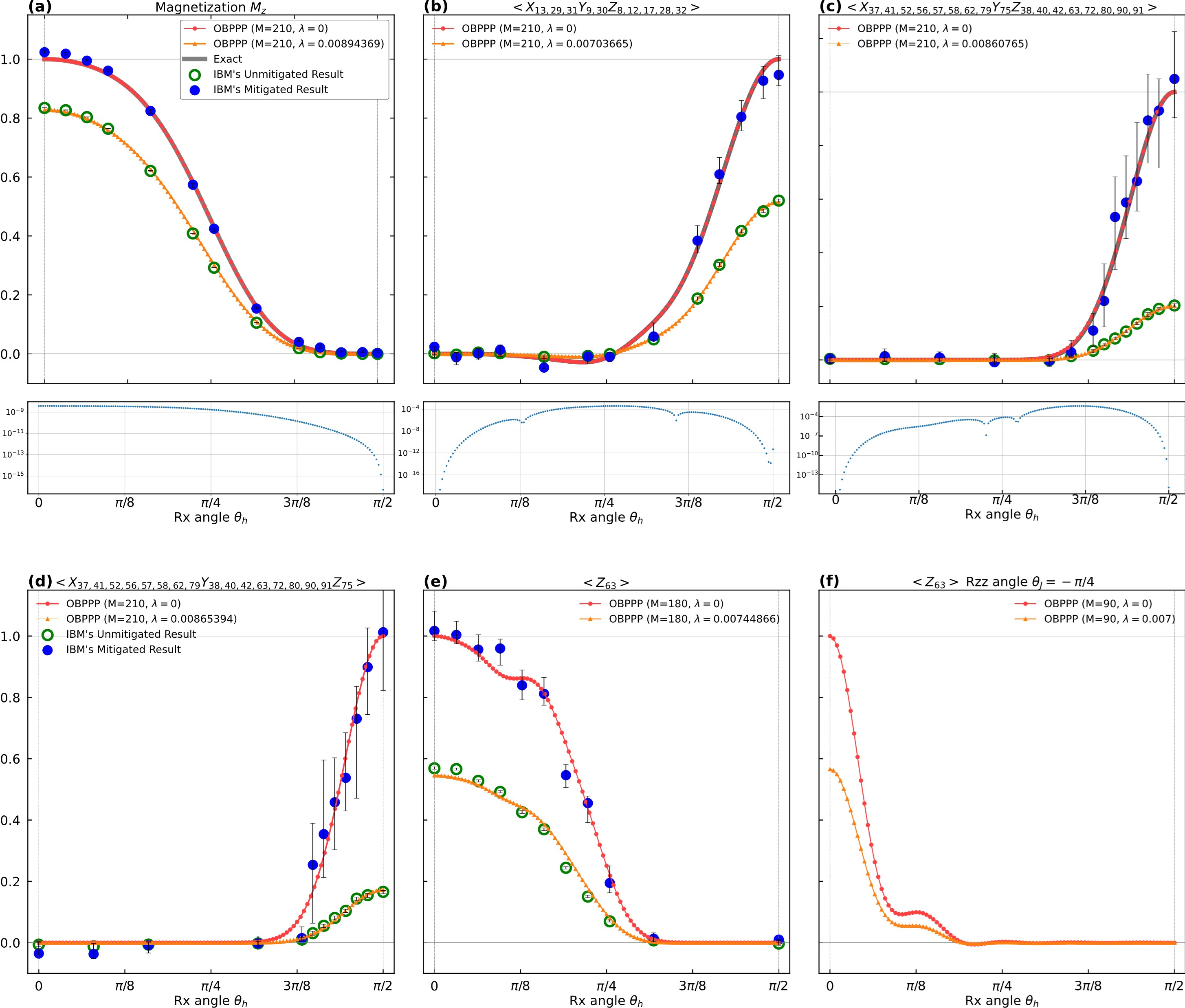
（figure; caption: the simulation results are consistent with the experimental results of the IBM Eagle quantum processor）

The researchers have successfully classically simulated the Eagle quantum computer at IBM, and have found significantly improvement for both the runtimes and the accuracy of the computed expectation values, when compared to conventional quantum hardware architecture. Taking the IBM simulation experiment as an example, where the parameters are n=127, L=80, the computational runtime through OBPPP is less than 5 minutes (based on the results of 2 Xeon6330 CPUs) for each diagram. In addition, the expectation values computed for varying noise rates can be seen to match impressively with the experimental results, in accordance to the noise suppression factor.

In summary, the authors of this work has developed the OBPPP method for classically simulating finite-depth variational quantum circuits. They have proven polynomial bounds on the computational complexity depending on the qubit number n and circuit depth L, which guaranteed polynomial computation time for the simulated expectation values for each given values of finite error tolerance and noise rate. Even in the presence of noise, this is a drastic improvement when compared to the usual quantum hardware architecture simulations, as demosntrated concretely by the numerical comparison with the IBM Eagle experiment. These results exhibits the applicability of this method in a wide range of quantum circuits. In addition, the work also sheds light on the relatinoship between noise and classical simulability.

This work was published in Physical Review Letters on September 18th, under the title "Simulating Noisy Variational Quantum Algorithms: A Polynomial Approach". The link to this work can be found here  https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.120603#fulltext

This work was completed jointly between researchers at BIMSA and YMSC. Yuguo Shao and Fuchuan Wei are doctoral students of YMSC as of 2020 and 2021, respectively. The corresponding authors, Zhengwei Liu and Song Cheng, are faculty members at BIMSA.

About Zhengwei Liu's group:

Research at Zhengwei Liu's group focuses the fields of quantum symmetries and quantum computing, and applies cutting-edge mathematical theory to the study of quantum theory. Among them, quantum error correction, quantum algorithm, quantum machine learning, quantum complexity, quantum programming and other core theories are key research subjects of the group. Currently, the team has established a new graphical language, Quon, for studying quantum information based on several topics of pioneering mathematics, including quantum topology, quantum algebra, quantum Fourier analysis. They have also proposed a new quantum communication protocol and quantum error correction design scheme based on this language.